A ray specifies a start point and a direction from the
point. So to define it requires two 3D vectors. A 3D vector to reperesent the
start point and a normalised (unit length) 3D vector to represent its direction.
mjbWorld uses rays for picking, i.e. when the mouse is pressed working out
which object to select.
how to generate ray
Once this ray has been generated we need to traverse through the scenegraph
to find, which objects intersect with the ray, and which of those objects are
closest to start of the ray (ie the viewpoint).
The following sections show how to determine if each type of node intersects
with the ray and then calculate the distance of the node from the start of the
ray.
In addition to the geometry nodes, we also need to consider the result of putting
the geometry nodes inside a Transform node. So for each of these nodes we need
to define a function which returns -1 if the ray does not intersect with the
node, and otherwise a positive number representing the distance from the start
of the ray to the node.
Sphere Node
We need to have a method to determine if a ray, if extended, would pass through
a sphere. This method is required for the picking routines in the program.
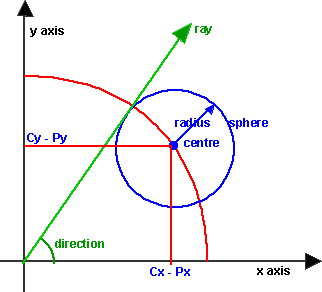
In the following assume all coordinates are measured relative to the start
point of the ray (ie the viewpoint/camera position). If you want to use absolute
coordinates the replace Cx, Cy, Cz with (Cx - Px), (Cy - Py), (Cz - Pz) and
Dx, Dy, Dz with (Dx - Px), (Dy - Py), (Dz - Pz) where Px, Py, Pz is the start
point of the ray.
The distance from P (start of ray) to the centre of the sphere is:
sqrt(Cx*Cx + Cy*Cy + Cz*Cz)
The ray, by definition, has unit length, so it we multiply it by the above
value it will be long enought to reach the sphere (if it is pointing in the
right direction). So if the original ray end point is:
| Dx |
| Dy |
| Dz |
Then when multiplied up the new end point is:
| Vx | = Dx * sqrt(Cx*Cx + Cy*Cy + Cz*Cz)
| Vy | = Dy * sqrt(Cx*Cx + Cy*Cy + Cz*Cz)
| Vz | = Dz * sqrt(Cx*Cx + Cy*Cy + Cz*Cz)
So the ray will pass through the sphere if V is inside the sphere.
The distance of V from C is:
sqrt( (Cx-Vx)^2 + (Cy-Vy)^2 + (Cy-Vy)^2)
if this is greater than R (the radius of the sphere) then the ray does not
pass through the sphere, so the test for intersection is:
R > sqrt( (Cx-Vx)^2 + (Cy-Vy)^2 + (Cy-Vy)^2)
Before we do this test, it is best to check whether, the start point is already
inside the sphere (in which case the ray must intersect) and then if the ray
is pointing away from the sphere (in which case ray cannot intersect). So the
test is as follows:
if (R > sqrt( (Cx)^2 + (Cy)^2 + (Cy)^2) return 0 // the start point is already
inside the sphere so the distance to it is zero
if (sqrt( (Cx-Vx)^2 + (Cy-Vy)^2 + (Cy-Vy)^2) > sqrt( Cx^2 + Cy^2 + Cy^2))
return -1 // the distance of the centre is greater than the distance to the
beginning so its pointing away
if (R < sqrt( (Cx-Vx)^2 + (Cy-Vy)^2 + (Cy-Vy)^2) return -1 // The distance
of V from C is greater than R so its outside
return sqrt(Cx*Cx + Cy*Cy + Cz*Cz) - R // return distance to the nearest point
The code for java is as follows:
void intersection(sfvec3f rayStart,sfvec3f rayDirection,sfnode nearestNode,sfvec3f distance) {
sfvec3f c = getSphereCentre().clone();
c.sub(rayStart); // c=centre of sphere relative to start of ray
double r = getSphereRadius(); // r=radius of sphere
double distanceToSphere = Math::sqrt((c.x * c.x) + (c.y * c.y) + (c.z * c.z));
if (r> distanceToSphere) { // the start point is already inside the sphere so the distance to it is zero
nearestNode.setNode(this);
distance.set(0.0);
return;
}
double vx = rayDirection.x * distanceToSphere;
double vy = rayDirection.y * distanceToSphere;
double vz = rayDirection.z * distanceToSphere; // v = end point of ray when projected to sphere orbit
double distanceFromEnd=Math::sqrt(((c.x - vx)*(c.x - vx)) + ((c.y - vy)*(c.y - vy)) + ((c.z - vz)*(c.z - vz)));
if (distanceFromEnd > distanceToSphere) return; // the distance of the centre is greater than the distance to the beginning so its pointing away
if (R < distanceFromEnd) return; // The distance of V from C is greater than R so its outside
double d=distance.getValue();
if ((d < 0.0) | (d > distanceToSphere - R)) {
distance.set(distanceToSphere - R); // return distance to the nearest point
nearestNode.setNode(this);
}
}
The code for managed C++ is as follows:
void sphereBean::intersection(sfvec3f* rayStart,sfvec3f* rayDirection,sfnode* nearestNode,sfvec3f* distance) {
sfvec3f* c = getSphereCentre()->clone();
c->sub(rayStart); // c=centre of sphere relative to start of ray
double r = getSphereRadius(); // r=radius of sphere
double distanceToSphere = Math::Sqrt((c->x * c->x) + (c->y * c->y) + (c->z * c->z));
if (r> distanceToSphere) { // the start point is already inside the sphere so the distance to it is zero
nearestNode->setNode(this);
distance->set(0.0);
return;
}
double vx = rayDirection->x * distanceToSphere;
double vy = rayDirection->y * distanceToSphere;
double vz = rayDirection->z * distanceToSphere; // v = end point of ray when projected to sphere orbit
double distanceFromEnd=Math::Sqrt(((c->x - vx)*(c->x - vx)) + ((c->y - vy)*(c->y - vy)) + ((c->z - vz)*(c->z - vz)));
if (distanceFromEnd > distanceToSphere) return; // the distance of the centre is greater than the distance to the beginning so its pointing away
if (R < distanceFromEnd) return; // The distance of V from C is greater than R so its outside
double d=distance->getValue();
if ((d < 0.0) | (d > distanceToSphere - R)) {
distance->set(distanceToSphere - R); // return distance to the nearest point
nearestNode->setNode(this);
}
}
Box Node
We need to have a method to determine if a ray, if extended, would pass through
a box. This method is required for the picking routines in the program.
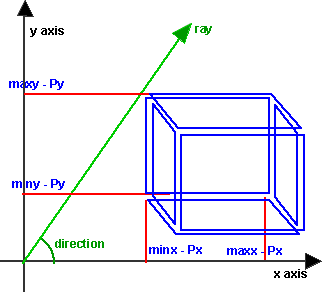
The method is to seperately test if the ray passes through each of the faces
of the box.
So, for each face, we extend the ray to the plane that the face is in, and
then test if the intersection point is inside the minimum and maximum dimeantions
of the box.
For the face at x==minx ,then we extend the ray to make Vx = minx, to keep
the ray pointing in the same direction we also have to multiply its other coodinates
by the same factor (minx / Dx).
| Vx | = Dx * minx / Dx = minx
| Vy | = Dy * minx / Dx
| Vz | = Dz * minx / Dx
so if
(Dy * minx / Dx < maxy) & (Dy * minx / Dx > miny) & (Dz * minx
/ Dx < maxz) & (Dz * minx / Dx > minz)
then the ray intersects with this face. So the following is the test for intersection
with all 6 faces:
((Dy * minx / Dx < maxy) & (Dy * minx / Dx > miny) & (Dz * minx
/ Dx < maxz) & (Dz * minx / Dx > minz)) |
((Dy * maxx / Dx < maxy) & (Dy * maxx / Dx > miny) & (Dz * maxx
/ Dx < maxz) & (Dz * maxx / Dx > minz)) |
((Dx * miny / Dy< maxx) & (Dx * miny / Dy> minx) & (Dz * miny
/ Dy< maxz) & (Dz * miny / Dy> minz)) |
((Dx * maxy / Dy< maxx) & (Dx * maxy / Dy> minx) & (Dz * maxy
/ Dy< maxz) & (Dz * maxy / Dy> minz)) |
((Dx * minz / Dz< maxx) & (Dx * minz / Dz> minx) & (Dy * minz
/ Dz< maxy) & (Dy * minz / Dz> miny)) |
((Dx * maxz / Dz< maxx) & (Dx * maxz / Dz> minx) & (Dy * maxz
/ Dz< maxy) & (Dy * maxz / Dz> miny))
As in the sphere example we first need to check if the ray starts inside the
box, and also if the ray is pointing away from the box.
So the full code is:
The code for java is as follows:
void intersection(sfvec3f rayStart,sfvec3f rayDirection,sfnode nearestNode,sfvec3f distance) {
double xmin = getWidth()/2 - rayStart.x;
double xmax = getWidth()/2 - rayStart.x;
double ymin = getHeight()/2 - rayStart.y;
double ymax = getHeight()/2 - rayStart.y;
double zmin = getDebth()/2 - rayStart.z;
double zmax = getDebth()/2 - rayStart.z;
if ((Dx < maxx) & (Dx > minx) & (Dy < maxy) & (Dy > miny) & (Dz < maxz) & (Dz > minz)) { // the start point is already inside the sphere so the distance to it is zero
nearestNode.setNode(this);
distance.set(0.0);
return;
}
double boxCentroidx = (xmax + xmin)/2;
double boxCentroidy = (ymax + ymin)/2;
double boxCentroidz = (zmax + zmin)/2;
double distanceToCentroid = Math::Sqrt(boxCentroidx*boxCentroidx + boxCentroidy*boxCentroidy + boxCentroidz*boxCentroidz);
double vx = rayDirection.x * distanceToCentroid;
double vy = rayDirection.y * distanceToCentroid;
double vz = rayDirection.z * distanceToCentroid; // v = end point of ray when projected to box orbit
double distanceFromEnd=Math::sqrt(((boxCentroidx - vx)*(boxCentroidx - vx)) + ((boxCentroidy - vy)*(boxCentroidy - vy)) + ((boxCentroidz - vz)*(boxCentroidz - vz)));
if (distanceFromEnd > distanceToCentroid) return; // the distance of the centre is greater than the distance to the beginning so its pointing away
if (((Dy * minx / Dx < maxy) & (Dy * minx / Dx > miny) & (Dz * minx / Dx < maxz) & (Dz * minx / Dx > minz)) |
((Dy * maxx / Dx < maxy) & (Dy * maxx / Dx > miny) & (Dz * maxx / Dx < maxz) & (Dz * maxx / Dx > minz)) |
((Dx * miny / Dy < maxx) & (Dx * miny / Dy > minx) & (Dz * miny / Dy < maxz) & (Dz * miny / Dy > minz)) |
((Dx * maxy / Dy < maxx) & (Dx * maxy / Dy > minx) & (Dz * maxy / Dy < maxz) & (Dz * maxy / Dy > minz)) |
((Dx * minz / Dz < maxx) & (Dx * minz / Dz > minx) & (Dy * minz / Dz < maxy) & (Dy * minz / Dz > miny)) |
((Dx * maxz / Dz < maxx) & (Dx * maxz / Dz > minx) & (Dy * maxz / Dz < maxy) & (Dy * maxz / Dz > miny))) return -1.0; // The distance of V from C is greater than R so its outside
double d=distance.getValue();
if ((d < 0.0) | (d > distanceToCentroid)) {
distance.set(distanceToCentroid); // I really want to return distance to the nearest point not the centrod is there a way to do this
nearestNode.setNode(this);
}
}
The code for managed C++ is as follows:
void boxBean::intersection(sfvec3f* rayStart,sfvec3f* rayDirection,sfnode* nearestNode,sfvec3f* distance) {
double xmin = getWidth()/2 - rayStart->x;
double xmax = getWidth()/2 - rayStart->x;
double ymin = getHeight()/2 - rayStart->y;
double ymax = getHeight()/2 - rayStart->y;
double zmin = getDebth()/2 - rayStart->z;
double zmax = getDebth()/2 - rayStart->z;
if ((Dx < maxx) & (Dx > minx) & (Dy < maxy) & (Dy > miny) & (Dz < maxz) & (Dz > minz)) { // the start point is already inside the sphere so the distance to it is zero
nearestNode->setNode(this);
distance->set(0.0);
return;
}
double boxCentroidx = (xmax + xmin)/2;
double boxCentroidy = (ymax + ymin)/2;
double boxCentroidz = (zmax + zmin)/2;
double distanceToCentroid = Math::Sqrt(boxCentroidx*boxCentroidx + boxCentroidy*boxCentroidy + boxCentroidz*boxCentroidz);
double vx = rayDirection->x * distanceToCentroid;
double vy = rayDirection->y * distanceToCentroid;
double vz = rayDirection->z * distanceToCentroid; // v = end point of ray when projected to box orbit
double distanceFromEnd=Math::Sqrt(((boxCentroidx - vx)*(boxCentroidx - vx)) + ((boxCentroidy - vy)*(boxCentroidy - vy)) + ((boxCentroidz - vz)*(boxCentroidz - vz)));
if (distanceFromEnd > distanceToCentroid) return; // the distance of the centre is greater than the distance to the beginning so its pointing away
if (((Dy * minx / Dx < maxy) & (Dy * minx / Dx > miny) & (Dz * minx / Dx < maxz) & (Dz * minx / Dx > minz)) |
((Dy * maxx / Dx < maxy) & (Dy * maxx / Dx > miny) & (Dz * maxx / Dx < maxz) & (Dz * maxx / Dx > minz)) |
((Dx * miny / Dy < maxx) & (Dx * miny / Dy > minx) & (Dz * miny / Dy < maxz) & (Dz * miny / Dy > minz)) |
((Dx * maxy / Dy < maxx) & (Dx * maxy / Dy > minx) & (Dz * maxy / Dy < maxz) & (Dz * maxy / Dy > minz)) |
((Dx * minz / Dz < maxx) & (Dx * minz / Dz > minx) & (Dy * minz / Dz < maxy) & (Dy * minz / Dz > miny)) |
((Dx * maxz / Dz < maxx) & (Dx * maxz / Dz > minx) & (Dy * maxz / Dz < maxy) & (Dy * maxz / Dz > miny))) return; // The distance of V from C is greater than R so its outside
double d=distance->getValue();
if ((d < 0.0) | (d > distanceToCentroid)) {
distance->set(distanceToCentroid); // I really want to return distance to the nearest point not the centrod is there a way to do this
nearestNode->setNode(this);
}
}
Indexed Face Set Node
Can anyone help me with this?
Cylinder Node
Can anyone help me with this?
Cone Node
Can anyone help me with this?
Text Node
Can anyone help me with this?
Extrusion Node
Can anyone help me with this?
Elivationgrid Node
Can anyone help me with this?
Indexed Line Set Node
Can anyone help me with this?
Transform
We are traversing the scenegraph to find the objects which intersect the ray.
When we are transversing below a transform node, it is not very efficient to
transform all the nodes under the transform nodes just for this test. It is
more efficient to work in the local coordinates of the subnodes and instead
to transform the start and direction of the ray. The following is to work out
how to translate the ray:
Translation:
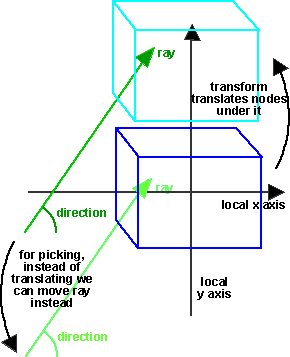
So under a Transform which is translated by (x,y,z) the equivalent ray is transformed
by:
Start Point: transform = (-x,-y,-z)
Direction: transform = (0,0,0)
Rotation:
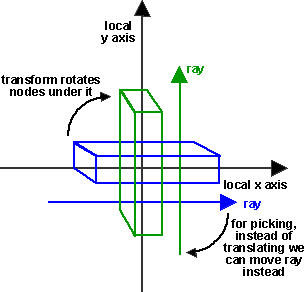
So under a Transform which is rotated by (x,y,z,angle) the equivalent ray is
transformed by:
Start Point: rotation = (x,y,z,-angle)
Direction: rotation = (x,y,z,-angle)
Scale:
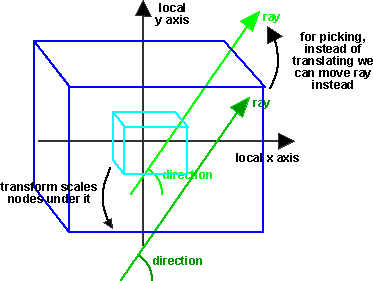
For scaling we need to scale the start point by the inverse factor, if the
scaling factor is the same in all directions then there is no need to alter
the direction, but if the scaling factors are different then we need to scale
by the inverse factor and then normalise.
So under a Transform which is scaled by (x,y,z) the equivalent ray is transformed
by:
Start Point: scale = (1/x,1/y,1/z)
Direction: scale = normalise(1/x,1/y,1/z)
Overall transform:
So the following gives the
The code for java is as follows:
void boxBean::intersection(sfvec3f rayStart,sfvec3f rayDirection,sfnode nearestNode,sfvec3f distance) {
sftransform transform = new sftransform();
transform.calcTransform(getTranslation(),getRotation(0),
getCenter(0),getScale(0),getScaleOrientation(0));
transform.invert();
sfvec3f localStart = new sfvec3f(rayStart);
transform.transform(localStart);
transform.m03 = 0.0;
transform.m13 = 0.0;
transform.m23 = 0.0;
sfvec3f localDirection = new sfvec3f(rayDirection);
transform.transform(localDirection);
for (int i=0;i<subnodes.get_Count();i++) {
nodeBean sgo = (nodeBean)(subnodes.get_Item(i));
sgo.intersection(localStart,localDirection,nearestNode,distance);
}
}
The code for managed C++ is as follows:
void transformGroupBean::intersection(sfvec3f* rayStart,sfvec3f* rayDirection,sfnode* nearestNode,sfvec3f* distance) {
sftransform* transform = new sftransform();
transform->calcTransform(getTranslation(),getRotation(0),
getCenter(0),getScale(0),getScaleOrientation(0));
transform->invert();
sfvec3f* localStart = new sfvec3f(rayStart);
transform->transform(localStart);
transform->m03 = 0.0;
transform->m13 = 0.0;
transform->m23 = 0.0;
sfvec3f* localDirection = new sfvec3f(rayDirection);
transform->transform(localDirection);
for (int i=0;i<subnodes->get_Count();i++) {
nodeBean* sgo = dynamic_cast<nodeBean*>(subnodes->get_Item(i));
sgo->intersection(localStart,localDirection,nearestNode,distance);
}
} |